第一篇算法博客,先写个简单的熟悉一下格式
题目来源于字节青训营稀土掘金网站上的算法题: 题库
问题描述
AB 实验同学每天都很苦恼如何可以更好地进行 AB 实验,每一步的流程很重要,我们目标为了缩短所需的步数。
我们假设每一步对应到每一个位置。从一个整数位置 x 走到另外一个整数位置 y,每一步的长度是正整数,每步的值等于上一步的值 -1, +0,+1。求 x 到 y 最少走几步。并且第一步必须是 1,最后一步必须是 1,从 x 到 y 最少需要多少步。
输入格式
输入包含 2 个整数 x,y。(0<=x<=y<2^31)
输出格式
对于每一组数据,输出一行,仅包含一个整数,从 x 到 y 所需最小步数。
输入样例
输出样例
我的答案:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| public class Main {
public static int solution(int xPosition, int yPosition) {
int footCount = 1;
int currentFootLength = 1;
System.out.println(currentFootLength);
int diff = (yPosition > xPosition) ? (yPosition - xPosition) : (xPosition - yPosition);
int currentFootSum = 1;
while (currentFootSum != diff) {
if (lateradd((currentFootLength),1) <= (diff-currentFootSum)){
currentFootLength ++;
System.out.println(currentFootLength);
} else if (lateradd(currentFootLength, 0) <= (diff-currentFootSum)){
System.out.println(currentFootLength);
} else if (lateradd(currentFootLength, -1) <= (diff-currentFootSum)){
currentFootLength --;
System.out.println(currentFootLength);
}
currentFootSum += currentFootLength;
footCount ++;
}
return footCount;
}
public static void main(String[] args) {
System.out.println(solution(12, 6) == 4);
System.out.println(solution(34, 45) == 6);
System.out.println(solution(50, 30) == 8);
System.out.println("Final Count:"+solution(0,23));
}
public static int lateradd(int current, int direction){
switch (direction) {
case 1:
return (current+1)*(current+2)/2;
case 0:
return (current)*(1+current)/2;
case -1:
return (current-1)*(current)/2;
default:
return 0;
}
}
}
|
总结
可见做算法题还是需要充分观察问题,输入和输出的结构,找出逻辑,以及利用已知的算法来套用问题。
(这次博客)也是有点简陋的,下次可以试着把代码块部分拆分成一个个小部分来讲,但是又不能让别人直接CV,很难受。要是有功能能折叠全代码就好了,或者把全代码放在最后?算了先按心情写把哈哈。
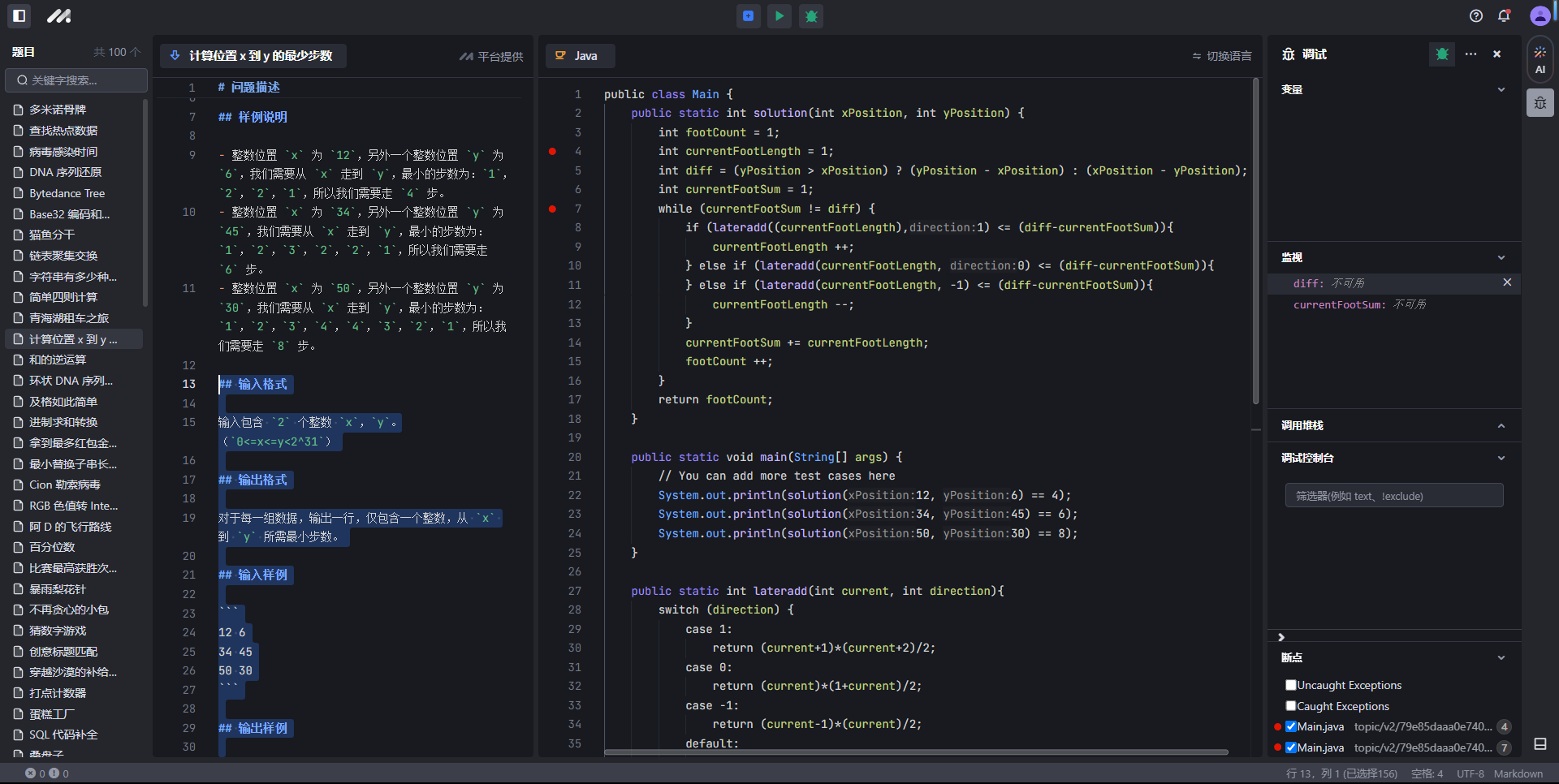
最后附一张字节那个稀土掘金的编译器图,旁边就是AI可以问,难绷。

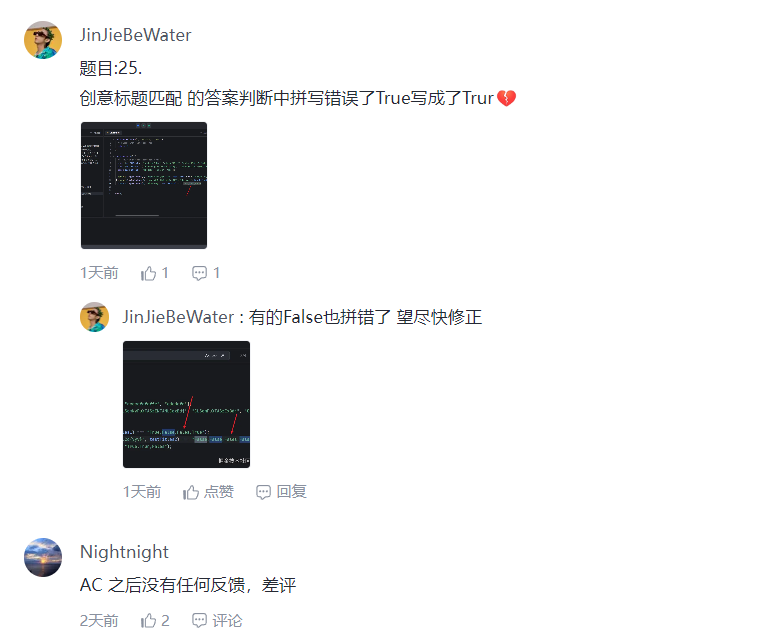
还是有很多人吐槽这个编译器和题目的。而且调试貌似还有点问题。